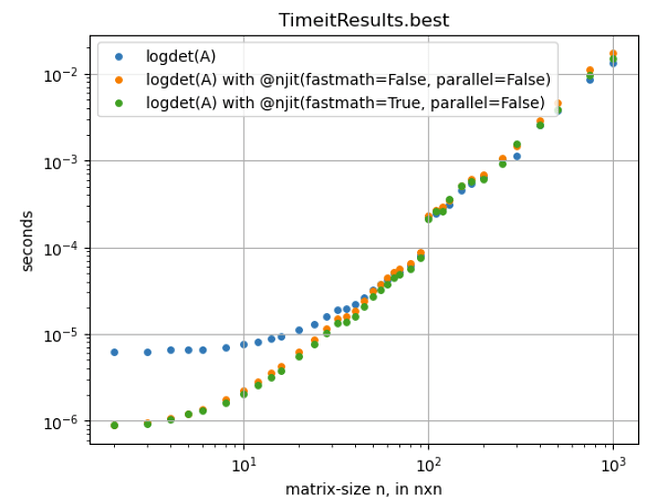
Hi,
I am learning how to use numba more in a numpy & scipy-based computation. The step numpy.linalg.slogdet(A) seems to be the second most time-consuming line (, slightly faster than this ), where A is a matrix of float64, different sizes in every run, ranging mostly from 1x1 to 300x300, a few times up to 600x600. I ran some %timeit-tests shown in the plot below and compiling clearly helps. Though only for matrix-sizes < 100x100.
From what I read so far, I think this is because the internal numpy-vectorization is already efficient. Is this correct? If not, how should I interpret the %timeit-results for sizes > 100x100?
RE
from numpy.linalg import slogdet
from numba import njit
def logdet(A):
sign, logabsdet = slogdet(A)
result = sign*logabsdet
return result
@njit(fastmath=False, parallel=False)
def logdet_numba(A):
sign, logabsdet = slogdet(A)
result = sign*logabsdet
return result
@njit(fastmath=True, parallel=False)
def logdet_numba_fm(A):
sign, logabsdet = slogdet(A)
result = sign*logabsdet
return result
ldbest = []
ldnbest = []
ldnfmbest = []
sizes = np.array(
(2, 3, 4, 5, 6, 8, 10, 12, 14, 16, 20, 24, 28, 32, 36, 40, 45, 50, 55, 60, 65,
70, 80, 90, 100, 110, 120, 130, 150, 170, 200, 250, 300, 400, 500, 750, 1000)
)
for n in sizes:
a = np.random.randn(n,n)
A = a.T@a
rld = %timeit -o -q logdet(A)
ldbest.append(rld.best)
rldn = %timeit -o -q logdet_numba(A)
ldnbest.append(rldn.best)
rldnfm = %timeit -o -q logdet_numba_fm(A)
ldnfmbest.append(rldnfm.best)
s = 12
plt.scatter(sizes, ldbest, s=s, label='logdet(A)');plt.yscale('log');plt.xscale('log')
plt.scatter(sizes, ldnbest, s=s, label='logdet(A) with @njit(fastmath=False, parallel=False)');plt.yscale('log');plt.xscale('log')
plt.scatter(sizes, ldnfmbest,s=s,label='logdet(A) with @njit(fastmath=True, parallel=False)' );plt.yscale('log');plt.xscale('log')
plt.xlabel('matrix-size n, in nxn');plt.ylabel('seconds');plt.title('TimeitResults.best');plt.grid();plt.legend();plt.show()